Zebrafish pigementation
In our previous zebrafish tutorial, we have shown how dynamo goes beyond discrete RNA velocity vectors to continous RNA vector field functions. In this tutorial, we will demonstrate a set of awesome downsgtream differential geometry and dynamical systems based analyses, enabled by the differentiable vector field functions, to gain deep functional and predictive insights of cell fate transition during zebrafish pigementation (Saunders, et al. 2019).
With differential geometry analysis of the continous vector field fuctions, we can calculate the RNA Jacobian (see our primer on differential geometry), which is a cell by gene by gene tensor, encoding the gene regulatory network in each cell. With the Jacobian matrix, we can further derive the RNA acceleration, curvature, which are cell by gene matrices, just like gene expression dataset.
In general (see figure below), we can perform differential analyses and gene-set enrichment analyses based on top-ranked acceleration or curvature genes, as well as the top-ranked genes with the strongest self-interactions, top-ranked regulators/targets, or top-ranked interactions for each gene in individual cell types or across all cell types, with either raw or absolute values with the Jacobian tensor. Integrating that ranking information, we can build regulatory networks across different cell types, which can then be visualized with ArcPlot, CircosPlot, or other tools.
In this tutorial, we will cover following topics:
learn contionus RNA velocity vector field functions in different spaces (e.g. umap or pca space)
calculate RNA acceleration, curvature matrices (cell by gene)
rank genes based on RNA velocity, curvature and acceleration matrices
calculate RNA Jacobian tensor (cell by gene by gene) for genes with high PCA loadings.
rank genes based on the jacobian tensor, which including:
rank genes with strong postive or negative self-interaction (
divergenceranking)other rankings, ranking modes including
full_reg,full_eff,eff,regandintbuild and visualize gene regulatory network with top ranked genes
gene enrichment analyses of top ranked genes
visualize Jacobian derived regulatory interactions across cells
visualize gene expression, velocity, acceleration and curvature kinetics along pseudotime trajectory
learn and visualize models of cell-fate transitions
Import relevant packages
# !pip install dynamo-release --upgrade --quiet
import dynamo as dyn
# set white background
dyn.configuration.set_figure_params(background='white')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from gseapy.plot import barplot, dotplot
import warnings
warnings.filterwarnings('ignore')
/Users/xiaojieqiu/opt/anaconda3/envs/dynamo_mkl/lib/python3.9/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
Set the logging level. Various logging level can be setted according to your needs:
DEBUG: useful for dynamo development, show all logging information, including those debugging information
INFO: useful for most dynamo users, show detailed dynamo running information
WARNING: show only warning information
ERROR: show only exception or error information
CRITICAL: show only critical information
%matplotlib inline
from dynamo.dynamo_logger import main_info, LoggerManager
LoggerManager.main_logger.setLevel(LoggerManager.INFO)
Load processed data or data preprocessing
If you followed the zebrafish pigmentation tutorial, you can load the processed zebrafish adata object here for all downstream analysis.
adata = dyn.sample_data.zebrafish()
adata
|-----> Downloading data to ./data/zebrafish.h5ad
AnnData object with n_obs × n_vars = 4181 × 16940
obs: 'split_id', 'sample', 'Size_Factor', 'condition', 'Cluster', 'Cell_type', 'umap_1', 'umap_2', 'batch'
layers: 'spliced', 'unspliced'
adata = dyn.sample_data.zebrafish()
preprocessor = dyn.pp.Preprocessor(cell_cycle_score_enable=True)
preprocessor.preprocess_adata(adata, recipe='monocle')
dyn.tl.dynamics(adata, cores=3)
dyn.tl.reduceDimension(adata)
dyn.tl.cell_velocities(adata)
dyn.tl.cell_velocities(adata)
dyn.pl.streamline_plot(adata, color=['Cell_type'])
|-----> Downloading data to ./data/zebrafish.h5ad
|-----> Running monocle preprocessing pipeline...
|-----------> filtered out 14 outlier cells
|-----------> filtered out 12746 outlier genes
|-----> PCA dimension reduction
|-----> <insert> X_pca to obsm in AnnData Object.
|-----> computing cell phase...
|-----> [Cell Phase Estimation] completed [4.9675s]
|-----> [Cell Cycle Scores Estimation] completed [0.2288s]
|-----> [Preprocessor-monocle] completed [2.3514s]
|-----> dynamics_del_2nd_moments_key is None. Using default value from DynamoAdataConfig: dynamics_del_2nd_moments_key=False
|-----------> removing existing M layers:[]...
|-----------> making adata smooth...
|-----> calculating first/second moments...
|-----> [moments calculation] completed [16.3130s]
|-----> retrieve data for non-linear dimension reduction...
|-----> [UMAP] using X_pca with n_pca_components = 30
|-----> <insert> X_umap to obsm in AnnData Object.
|-----> [UMAP] completed [14.5781s]
|-----> incomplete neighbor graph info detected: connectivities and distances do not exist in adata.obsp, indices not in adata.uns.neighbors.
|-----> Neighbor graph is broken, recomputing....
|-----> Start computing neighbor graph...
|-----------> X_data is None, fetching or recomputing...
|-----> fetching X data from layer:None, basis:pca
|-----> method arg is None, choosing methods automatically...
|-----------> method ball_tree selected
|-----> 0 genes are removed because of nan velocity values.
|-----> [calculating transition matrix via pearson kernel with sqrt transform.] in progress: 100.0000%|-----> [calculating transition matrix via pearson kernel with sqrt transform.] completed [4.4069s]
|-----> [projecting velocity vector to low dimensional embedding] in progress: 100.0000%|-----> [projecting velocity vector to low dimensional embedding] completed [0.5564s]
|-----> 0 genes are removed because of nan velocity values.
Using existing pearson_transition_matrix found in .obsp.
|-----> [projecting velocity vector to low dimensional embedding] in progress: 100.0000%|-----> [projecting velocity vector to low dimensional embedding] completed [0.5448s]
|-----------> plotting with basis key=X_umap
|-----------> skip filtering Cell_type by stack threshold when stacking color because it is not a numeric type

If you confronted errors when saving dynamo processed adata object, please see the very end of this tutorial.
If you would like to start from scratch, use the following code to preprocess the zebrafish adata object (or use your own dataset):
adata = dyn.sample_data.zebrafish()
dyn.pp.recipe_monocle(adata)
dyn.tl.dynamics(adata, cores=3)
dyn.tl.reduceDimension(adata)
dyn.tl.cell_velocities(adata)
dyn.tl.cell_velocities(adata)
dyn.pl.streamline_plot(adata, color=['Cell_type'])
Differential geometry analysis
In this part we will demonstrate how to leverage dynamo to estimate RNA jacobian (reveals state-dependent regulation), RNA acceleration/curvature (reveals earlier drivers and fate decision points), etc.
To gain functional and biological insights, we can perform a series of downstream analysis with the computed differential geometric quantities. We can first rank genes across all cells or in each cell group for any of those differential geometric quantities, followed by gene set enrichment analyses of the top ranked genes, as well as regulatory network construction and visualization.
The differential geometry and dynamical systems (i.e. fixed points, nullclines, etc mentioned in the previous zebrafish tutorial) are conventionally used to describe small-scale systems, while the vector field we build comes from high-dimensional genomics datasets. From this, you can appreciate that with dynamo, we are bridging small-scale systems-biology/physics type of thinking with high-dimensional genomics using ML, something really unimaginable until very recently!
In order to calculate RNA jacobian, acceleration and curvature, we can either learn the vector field function directly in the gene expression space or on the PCA space but then project the differential geometric quantities learned in PCA space back to the original gene expression space. Since we often have thousands of genes, we generally learn vector field in PCA space to avoid the curse of dimensionality and to improve the efficiency and accuracy of our calculation.
Vector field learning in PCA space
To learn PCA basis based RNA velocity vector field function, we need to first project the RNA velocities into PCA space.
dyn.tl.cell_velocities(adata, basis='pca');
|-----> 0 genes are removed because of nan velocity values.
Using existing pearson_transition_matrix found in .obsp.
|-----> [projecting velocity vector to low dimensional embedding] in progress: 100.0000%|-----> [projecting velocity vector to low dimensional embedding] completed [0.5750s]
Then we will use the dyn.vf.VectorField function to learns the
vector field function in PCA space. This function relies on
sparseVFC
to learn the high dimensional vector field function in the entire
expression space from sparse single cell velocity vector samples
robustly.
Note that if you don’t provide any basis, vector field will be learned in the original gene expression and you can learn vector field for other basis too, as long as you have the RNA velocities projected in that basis.
Related information for the learned vector field are stored in adata.
dyn.vf.VectorField(adata,
basis='pca',
M=100)
|-----> VectorField reconstruction begins...
|-----> Retrieve X and V based on basis: PCA.
Vector field will be learned in the PCA space.
|-----> Learning vector field with method: sparsevfc.
|-----> [SparseVFC] begins...
|-----> Sampling control points based on data velocity magnitude...
|-----> [SparseVFC] completed [0.0670s]
|-----> [VectorField] completed [0.1500s]
Velocity, acceleration and curvature ranking
To gain functional insights of the biological process under study, we design a set of ranking methods to rank gene’s absolute, positive, negative vector field quantities in different cell groups that you can specify. Here we will first demonstrate how to rank genes based on their velocity matrix.
Basically, the rank functions in the vector field submodule (vf) of dynamo is organized as rank_{quantities}**_genes** where {quantities} can be any differential geometry quantities, including, velocity, divergence, acceleration, curvature, jacobian:
dyn.vf.rank_velocity_genes(adata, groups=‘Cell_type’)
dyn.vf.rank_divergence_genes(adata, groups=‘Cell_type’)
dyn.vf.rank_acceleration_genes(adata, groups=‘Cell_type’)
dyn.vf.rank_curvature_genes(adata, groups=‘Cell_type’)
dyn.vf.rank_jacobian_genes(adata, groups=‘Cell_type’)
Gene ranking for different quantities (except jacobian, see below)
are done based on both their raw and absolute velocities for each cell
group when groups is set or for all cells if it is not set.
dyn.vf.rank_velocity_genes(adata,
groups='Cell_type',
vkey="velocity_S");
Ranking results are saved in .uns with the pattern
rank_{quantities}_genes or
rank_abs_{quantities}**_genes** where {quantities} can be
any differential geometry quantities and the one with _abs indicates
the ranking is based on absolute values instead of raw values.
We can save the speed ranking information to rank_speed or
rank_abs_speed for future usages if needed.
rank_speed = adata.uns['rank_velocity_S'];
rank_abs_speed = adata.uns['rank_abs_velocity_S'];
Next we usedyn.vf.acceleration to compute acceleration for each
cell with the learned vector field in adata. Note that we use PCA basis
to calculate acceleration, but dyn.vf.acceleration will by default
project acceleration_pca back to the original high dimension
gene-wise space. You can check the resulted adata which will have both
acceleration (in .layers) and acceleration_pca (in .obsm).
We can also rank acceleration in the same fashion as what we did to
velocity.
dyn.vf.acceleration(adata, basis='pca')
|-----> [Calculating acceleration] in progress: 100.0000%|-----> [Calculating acceleration] completed [0.1028s]
dyn.vf.rank_acceleration_genes(adata,
groups='Cell_type',
akey="acceleration",
prefix_store="rank");
rank_acceleration = adata.uns['rank_acceleration'];
rank_abs_acceleration = adata.uns['rank_abs_acceleration'];
Similarly, we can also use dyn.vf.curvature to calculate curvature
for each cell with the reconstructed vector field function stored in
adata. dyn.vf.rank_curvature_genes ranks genes based on their raw or
absolute curvature values in different cell groups.
dyn.vf.curvature(adata, basis='pca');
|-----> [Calculating acceleration] in progress: 100.0000%|-----> [Calculating acceleration] completed [0.1112s]
|-----> [Calculating curvature] in progress: 100.0000%|-----> [Calculating curvature] completed [0.1405s]
dyn.vf.rank_curvature_genes(adata, groups='Cell_type');
Now we estimated RNA acceleration and RNA curvature, we can
visualize the acceleration or curvature for individual genes just like
what we can do with gene expression or velocity, etc.
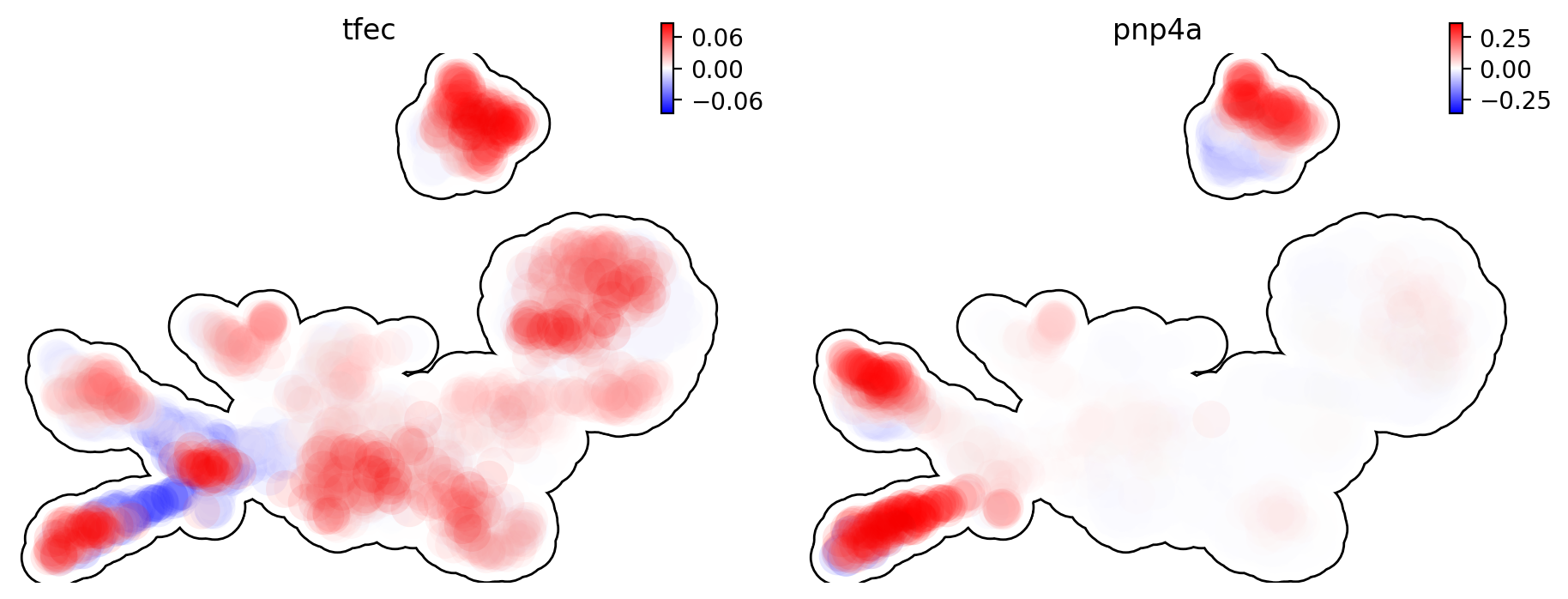
Let us show the velocity for gene tfec and pnp4a. bwr
(blue-white-red) colormap is used here because velocity has both
positive and negative values. The same applies to acceleration and
curvature.
dyn.pl.umap(adata, color=['tfec', 'pnp4a'], layer='velocity_S', frontier=True)
|-----------> plotting with basis key=X_umap
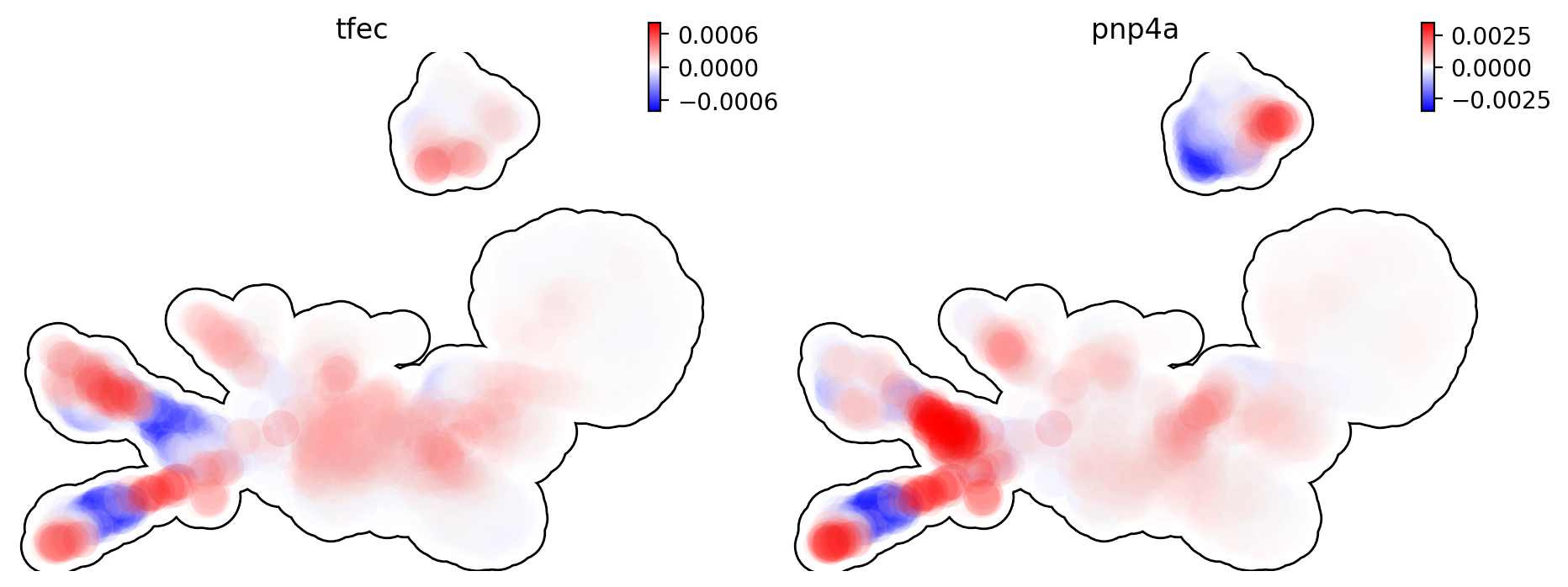
This is for acceleration of genes tfec and pnp4a.
dyn.pl.umap(adata, color=['tfec', 'pnp4a'], layer='acceleration', frontier=True)
|-----------> plotting with basis key=X_umap
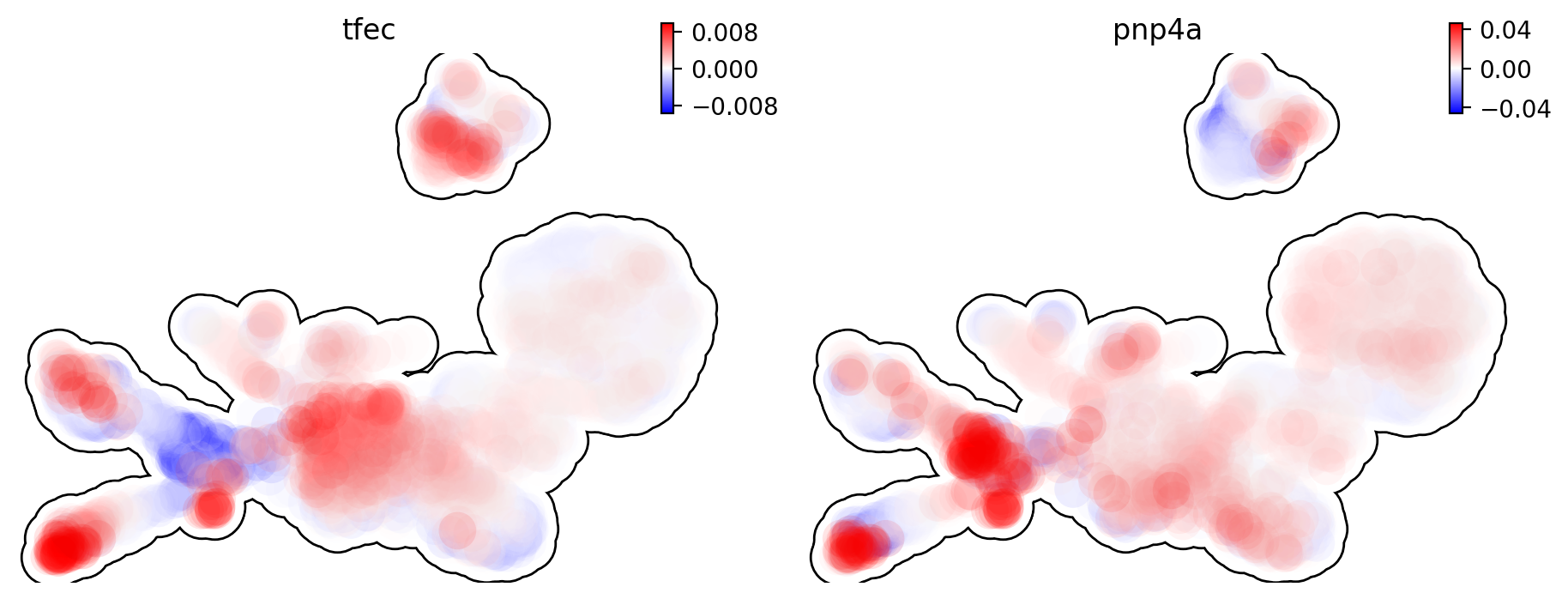
This is for curvature of genes tfec and pnp4a.
dyn.pl.umap(adata, color=['tfec', 'pnp4a'], layer='curvature', frontier=True)
|-----------> plotting with basis key=X_umap
The purpose for us to develop vaious differential geometry analyses is to derive functional predictions. So let us work on this a little bit next.
Gene set enrichment
In this ection, we show our first approach to reveal functional insights
with the dyn.ext.enrichr function implemented in dynamo, a
python wrapper for Enrichr, to identify biological pathways with
statistical significance.
We noticed that the previous study (Saunders, et al. 2019) reported a “unknown” cell type from their conventional markers based cell-typing method based on total RNA expression levels. We wonder whether we can unveil its cell-type identify with dynamo. Therefore, we perform gene set enrichment analysis with the top-ranked genes with the highest absolute acceleration from this previously “unknown” cell type. Interestingly, we found the genes were enriched in chondrocyte-related pathways, indicative of a potential chondrocytic origin.
enr = dyn.ext.enrichr(adata.uns['rank_abs_acceleration']['Unknown'][:250].to_list(), organism='Fish', outdir='./enrichr', gene_sets='GO_Biological_Process_2018')
dotplot(enr.res2d, title='abs acceleration ranking', cmap='viridis_r', cutoff=0.1)
<Axes: title={'center': 'abs acceleration ranking'}, xlabel='Combined Score'>
Jacobian Calculation and Ranking
Next we will calculate Jacobian for each cell with the reconstructed
vector field. If we use PCA space, dyn.vf.jacobian can project the
low dimension Jacobian results back to high dimension to get a cell by
gene by gene tensor. You can check the jacobian_gene key from the
.uns["jacobian_pca"] dictionary in the resulted adata object to
confirm this.
The cell by gene by gene tensor is generally huge, especially for
datasets with large number of cells. We thus would love to do some
preprocessing to alleviate the burden of computational resource
requirements, either by restricting the calculation to genes that have
high loading in our pca analysis or by downsampling the cells that will
be used to calculate the jacobian matrix in each cell.
For the first one, we will use dyn.pp.top_pca_genes to calculate
top_pca_genes for adata, according to PCs loading in adata.uns.
Note that n_top_genes below means we take the union of genes with
top n absolute values for each principal components, so the
resulting PCA genes may be larger than 100.
For the second one, we can use the following parameters in
dyn.vf.jacobian.
sampling=None,
sample_ncells=1000,
When the sampling is choosen from one of the
'random', 'velocity', 'trn', the function will sample
sample_ncells accord to the sampling method sample for the
Jacobian matrix calculation in only sample_ncells sampled cells. We
recommend dynamo users to start considering sampling cells with your
adata object with more than 2500 cells while the top pca gene selected
will be around 500.
dyn.pp.top_pca_genes(adata, n_top_genes=100);
Select top pca genes (flagged in top_pca_genes in .var after
running pp.top_pca_genes) and use those genes to set the
regulator/effectors that are necessary in cell-wise jacobian matrix
calculation.
top_pca_genes = adata.var.index[adata.var.top_pca_genes];
Here we will ensure a set of the chondrocyte-related gene included in
the Jacobian calculation so that we can visualize the regulatory network
for those genes. You can include other set of genes you care about as
long as they are genes used for pca dimension reduction, that is
adata[:, genes].var.use_for_pca are all True.
top_pca_genes = ["erbb3b", "col6a3", "vwa1", "slc35c2", "col6a2", "col6a1"] + list(top_pca_genes)
dyn.vf.jacobian(adata, regulators=top_pca_genes, effectors=top_pca_genes);
Transforming subset Jacobian: 100%|████████| 4181/4181 [00:26<00:00, 160.39it/s]
We can take advantage of the cell-wise jacobian matrix to
investigate gene regulation at single-cell resolution or a
state-dependent fashion.
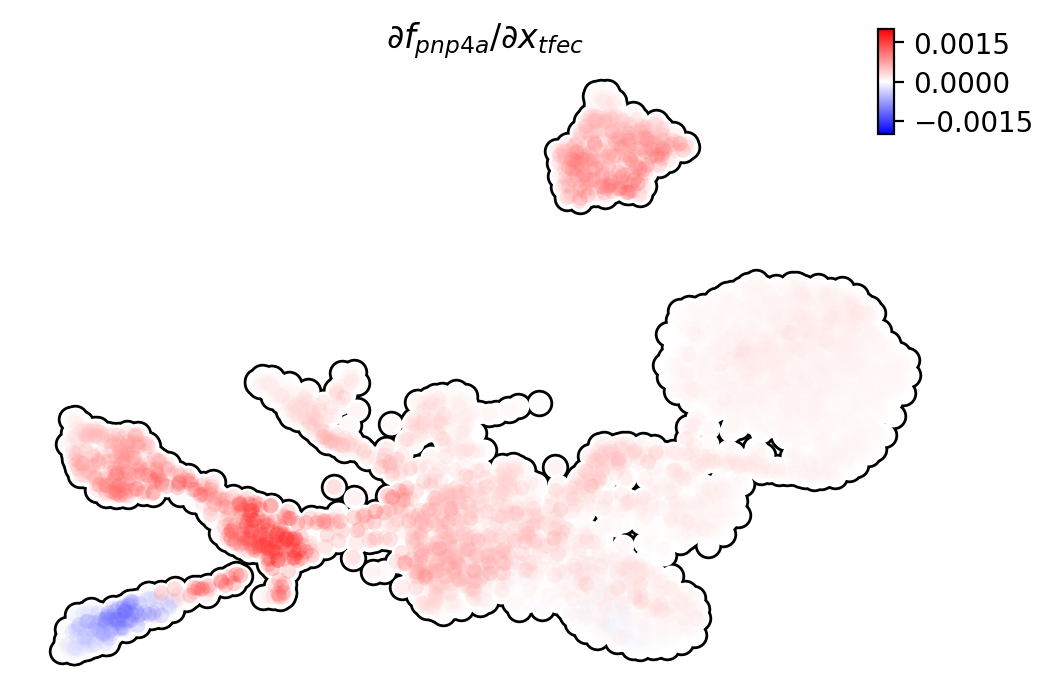
In iridophore cells, we found that pnp4a was potentially activated
by tfec in the progenitors of iridophore lineage which is in line
with that reported in Petratou et al. 2021. Futhermore, there seem to
have a possible repression occurring when tfec expression level was high
in the mature iridophore cells.
We can visualize the regulation from tfec to pnp4a
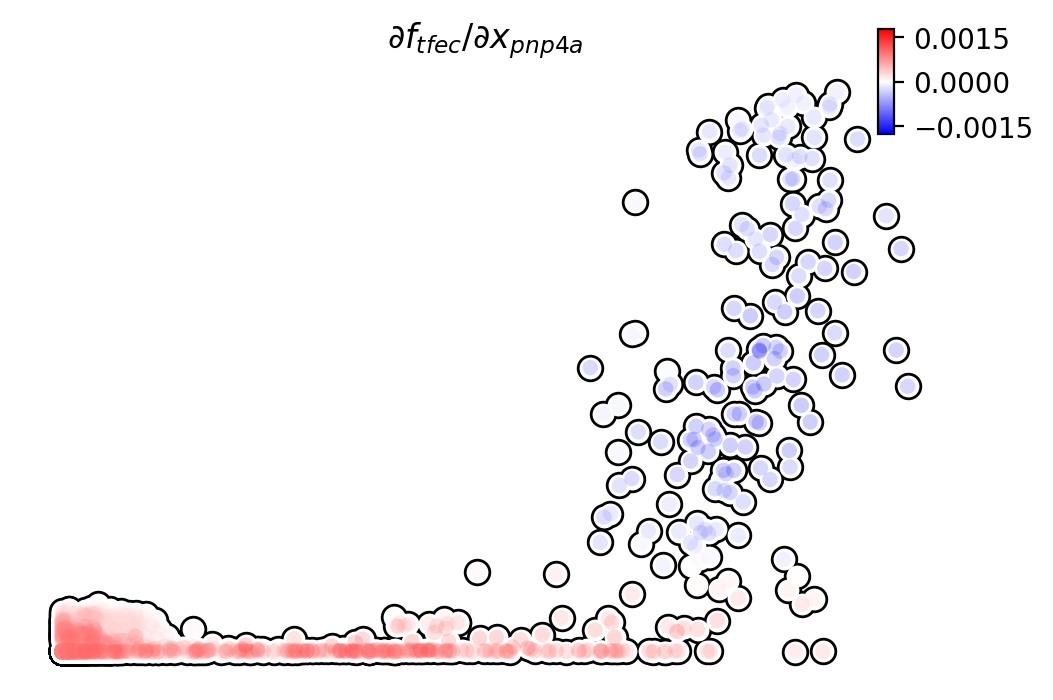
(\(\frac{\partial f_{pnp4a}}{\partial f_{tfec}}\)) on the umap
embedding. \(\frac{\partial f_{pnp4a}}{\partial f_{tfec}}\) denotes
the effects of changing the expression of tfec to the velocity of
pnp4a.
dyn.pl.jacobian(adata, regulators=['tfec'], effectors=['pnp4a'], basis='umap')

Similarly, we can also visualize the regulation from tfec to
pnp4a (\(\frac{\partial f_{pnp4a}}{\partial f_{tfec}}\)) on top
of the gene expression level of tfec (x-axis) to pnp4a
(y-axis).
dyn.pl.jacobian(adata, regulators=['pnp4a'], effectors=['tfec'], x='tfec', y="pnp4a", layer='M_s', basis='umap')
Ranking for Jacobian matrices
After estimating the cell-wise Jacobian matrix, we now demonstrate different ways to rank genes based on the Jacobian matrix with dynamo.
We start with the so-called “divergence” ranking for each cell group.
The “divergence” we are talking about here is different from the
definition of divergence which is basically the sum of the diagonal
elements of the Jacobian. Instead the divergence in this context
points to the self-activation or self-inhibition terms.
The results of divergence ranking are stored in
adata.uns['rank_div_gene_jacobian_pca'].
divergence_rank = dyn.vf.rank_divergence_genes(adata, groups='Cell_type');
We can rank all other elements in the Jacobian. There are 5 parameters
we provide in dyn.vf.rank_jacobian_genes’s argument list to rank
the Jacobian:
“full reg” or “full_reg”: top regulators are ranked for each effector for each cell group
“full eff” or “full_reff”: top effectors are ranked for each regulator for each cell group
“reg”: top regulators in each cell group
“eff”: top effectors in each cell group
“int”: top effector-regulator pairs in each cell group
Note that the default mode is “full reg”. More details can be found on
API pages of online documentation. dyn.vf.rank_jacobian_genes
full_reg_rank = dyn.vf.rank_jacobian_genes(adata,
groups='Cell_type',
mode="full_reg",
abs=True,
output_values=True,
return_df=True)
full_eff_rank = dyn.vf.rank_jacobian_genes(adata,
groups='Cell_type',
mode='full_eff',
abs=True,
exclude_diagonal=True,
output_values=True,
return_df=True)
The results of full_eff and full_reg are dictionaries, whose keys are
cluster (cell type in the case above) names and values are
pd.DataFrame with rank information as well as coefficient values
stored for each gene. See below:
type(full_reg_rank)
dict
print(full_reg_rank['Unknown'].shape)
full_reg_rank["Unknown"].head(2)
(467, 934)
| tmsb4x | tmsb4x_values | rplp2l | rplp2l_values | rpl7a | rpl7a_values | pvalb1 | pvalb1_values | gfap | gfap_values | ... | slc4a4a | slc4a4a_values | ccna2 | ccna2_values | ddc | ddc_values | top2a | top2a_values | slc6a2 | slc6a2_values | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | si:dkey-183i3.5 | 0.001557 | si:dkey-183i3.5 | 0.001826 | si:dkey-183i3.5 | 0.001525 | si:dkey-183i3.5 | 0.001295 | mt2 | 0.001241 | ... | mt2 | 0.000326 | hmgn2 | 0.001233 | tubb5 | 0.000438 | hmgn2 | 0.000979 | tubb5 | 0.000425 |
| 1 | zgc:136930 | 0.001212 | calm2b | 0.001520 | calm2b | 0.001270 | mcl1b | 0.001133 | gfap | 0.001165 | ... | gfap | 0.000276 | hmgb2a | 0.000899 | elavl4 | 0.000422 | hmgb2a | 0.000703 | elavl4 | 0.000409 |
2 rows × 934 columns
From the above table, we can see that in the previously “Unknown” cell
type, the top two regulators of tmsb4x gene (the first column in the
above table) are mbpb and si:ch211-156j16.1 with their aggregate
regulation strength based on Jacobian 0.001429 and 0.001422,
respectively. The same applies to other columns and similarly to the
full_eff_rank dictionary.
eff_rank = dyn.vf.rank_jacobian_genes(adata, groups='Cell_type', mode='eff', abs=True, output_values=True)
reg_rank = dyn.vf.rank_jacobian_genes(adata, groups='Cell_type', mode='reg', abs=True, exclude_diagonal=True)
int stands for interactions, the pairs of (gene1, gene2) values in
jacobian matrix.
int_rank = dyn.vf.rank_jacobian_genes(adata, groups='Cell_type', mode='int', exclude_diagonal=True, output_values=True)
Construct and visualize cell-type specific regulatory networks
With the full_reg_rank and full_eff_rank calculated, we can now
pass a set of genes of interests and use them to build a regulatory
network for any specific cell type and then visualize the network with
either an arcPlot or a circosPlot, etc.
We build networks for each cell type by passing the argument
cluster = "Cell_type" to dyn.vf.build_network_per_cluster
function. The edges and their weights are based on the above ranking
full regulator/effector dictionaries (pass as values to the
full_reg_rank and full_eff_rank arguments).
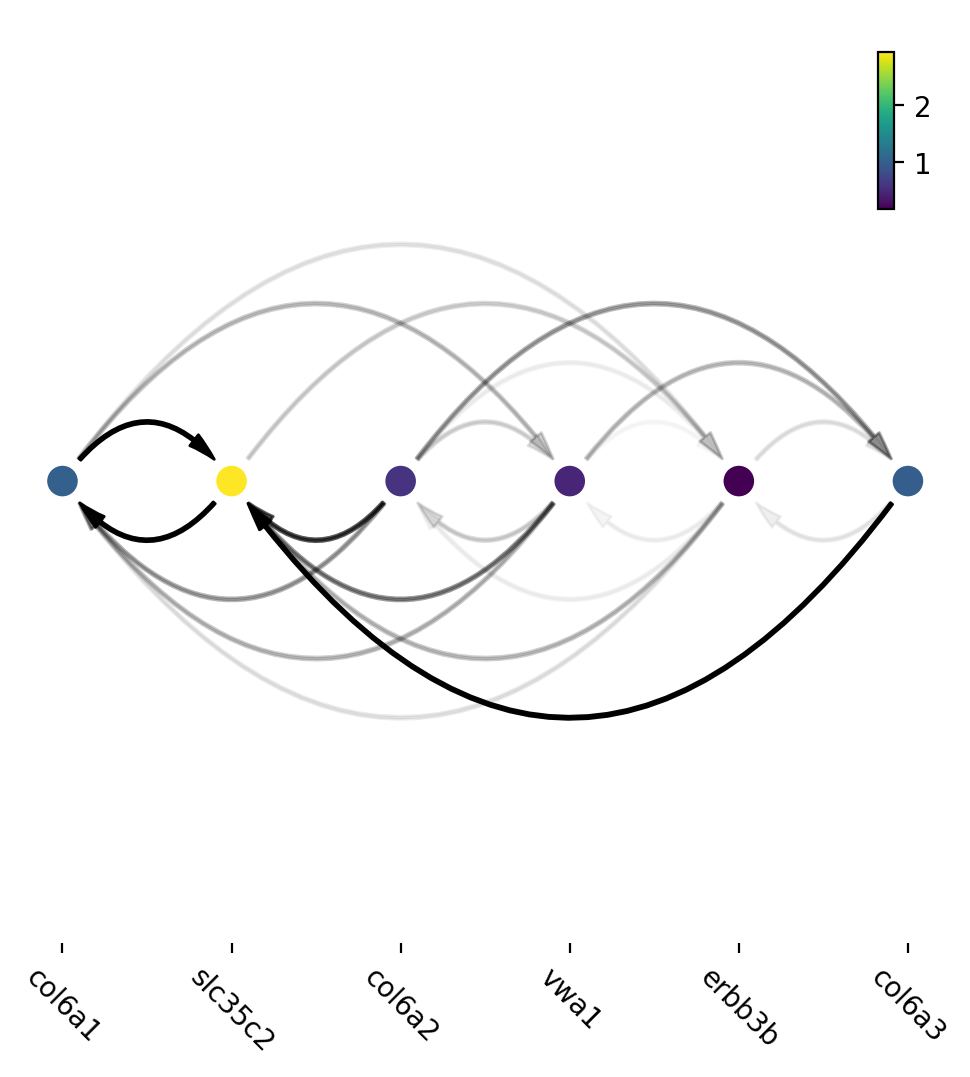
Interesting, Jacobian analysis revealed potential regulation of the
chondrocyte marker slc36c2 by the pigment regulator erbb3,
consistent with previous reports that EGFR (erbb3) signaling is
critical for maintaining the chondrocyte lineage (Fisher et al. 2007).
In addition, this analysis revealed a strong connection between
chondrocyte-specific markers col6a3, col6a, col6a2, and
vwa1.
Here we will use a few key gene in the “unknown” cell cluster to build a regulatory network based on the estimated cell-wise Jacobian matrices of chondrocyte cells.
unknown_cell_type_regulators = ["erbb3b", "col6a3", "vwa1", "slc35c2", "col6a2", "col6a1"]
edges_list = dyn.vf.build_network_per_cluster(adata,
cluster='Cell_type',
cluster_names=None,
full_reg_rank=full_reg_rank,
full_eff_rank=full_eff_rank,
genes=np.unique(unknown_cell_type_regulators),
n_top_genes=100)
import networkx as nx
network = nx.from_pandas_edgelist(edges_list['Unknown'], 'regulator', 'target', edge_attr='weight', create_using=nx.DiGraph())
|-----> [iterating reg_groups] in progress: 100.0000%|-----> [iterating reg_groups] completed [1.3277s]
Network can then be visualized as an Arcplot:
ax=dyn.pl.arcPlot(adata, cluster="Cell_type", cluster_name="Unknown", edges_list=None, network=network, color="M_s")
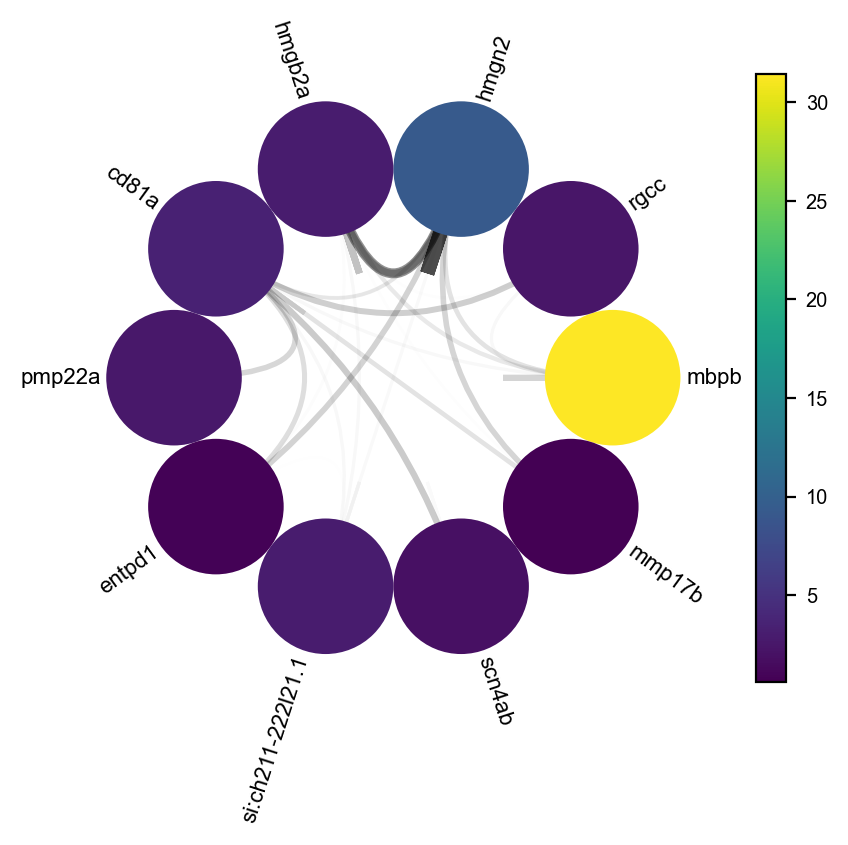
Similarly, network can also be built with other criteria and visualized
with other plots, like the circos plot or hive Plot. For example, we can
select 10 top genes with highest absolute acceleration values in
Unknown cell type.
selected_genes = adata.uns['rank_abs_acceleration']['Unknown'][:10]
edges_list = dyn.vf.build_network_per_cluster(adata,
cluster='Cell_type',
cluster_names=None,
full_reg_rank=full_reg_rank,
full_eff_rank=full_eff_rank,
genes=selected_genes,
n_top_genes=1000)
|-----> [iterating reg_groups] in progress: 100.0000%|-----> [iterating reg_groups] completed [1.4511s]
We can then focus on analyzing Unknown cell type network and
construct networkx graph structure for Unknown cell group. We next
constrain the edges by removing all edges with weight <= 0.0015.
network = nx.from_pandas_edgelist(edges_list['Unknown'].drop_duplicates().query("weight > 0.0015"),
'regulator', 'target',
edge_attr='weight',
create_using=nx.DiGraph())
Before drawing a circos plot, we can insert attributes into networkx
Graph object. In the code cell below, we assign average M_s
values to each cluster to color the nodes in the circos plot later.
color_key = "M_s"
cluster_key = "Cell_type"
selected_cluster = "Unknown"
adata_layer_key = "M_s"
for node in network.nodes:
network.nodes[node]["M_s"] = adata[:, node].layers["M_s"].mean()
for edge in network.edges:
network.edges[edge]["weight"] *= 1000
Lastly, we can visulize the network with dyn.pl.circosPlot.
dyn.configuration.set_figure_params(background='white')
dyn.pl.circosPlot(network, node_color_key="M_s", show_colorbar=True, edge_alpha_scale=0.7, edge_lw_scale=0.7)
<Axes: >
Visualize gene expression, velocity, acceleration, curvature as a function of vector field based pseudotime.
Here we can apply ddhodge to first obtain a measure of pseudotime
that is based on learned vector field function. Then we can visualize
gene expression, velocity, acceleration, curvature as a function of
vector field based pseudotime to reveal different aspects of gene
expression kinetics over time.
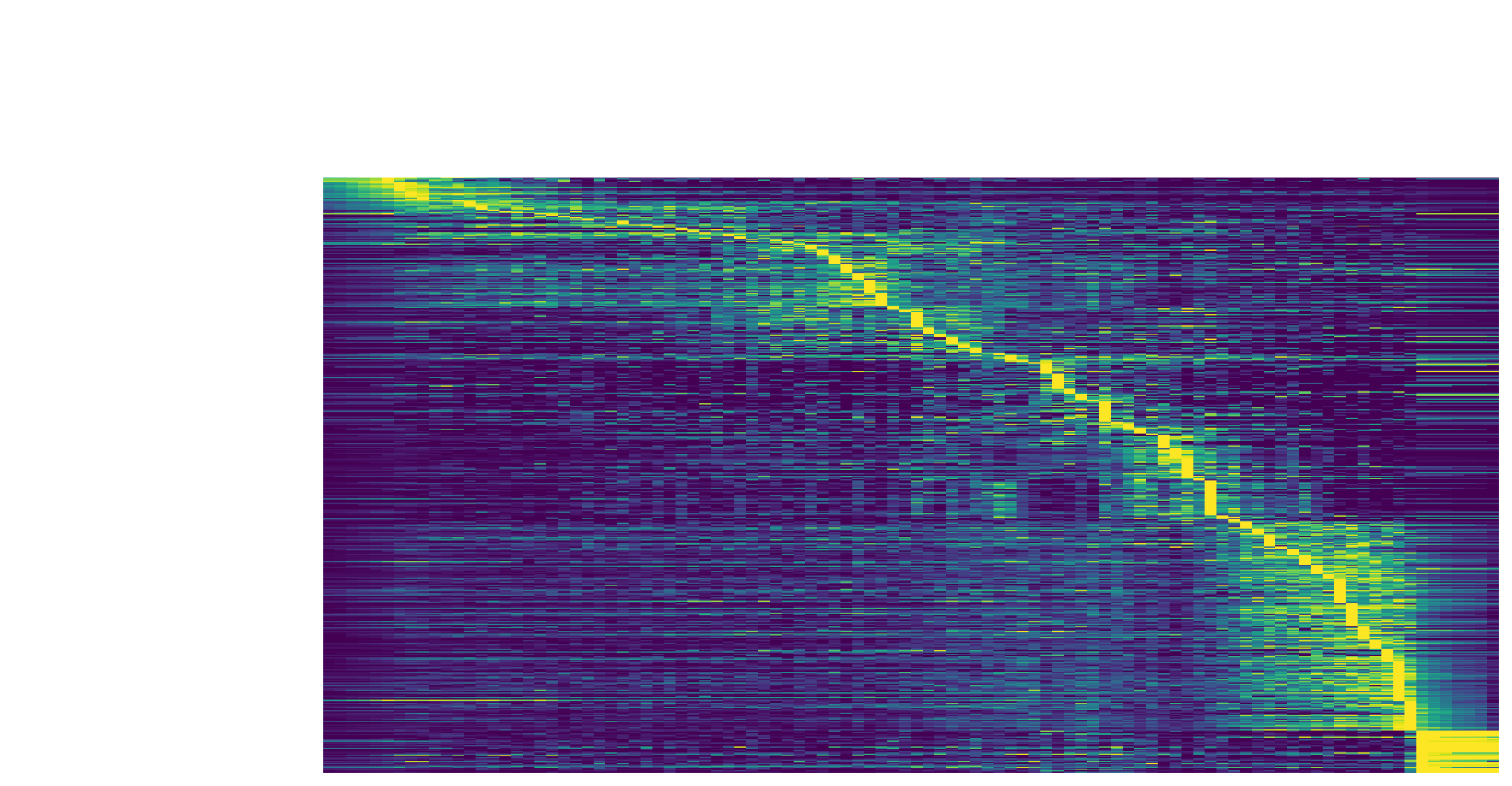
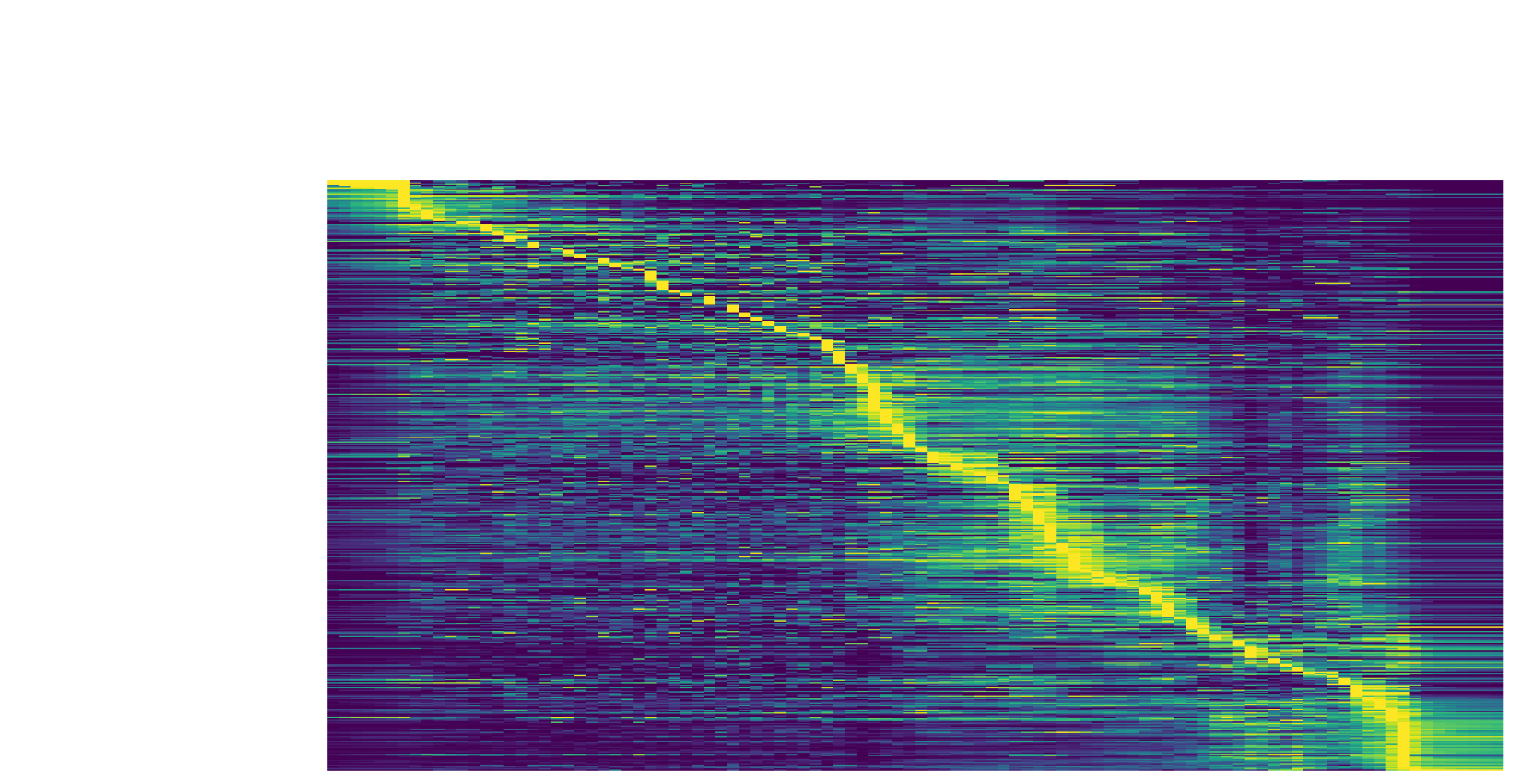
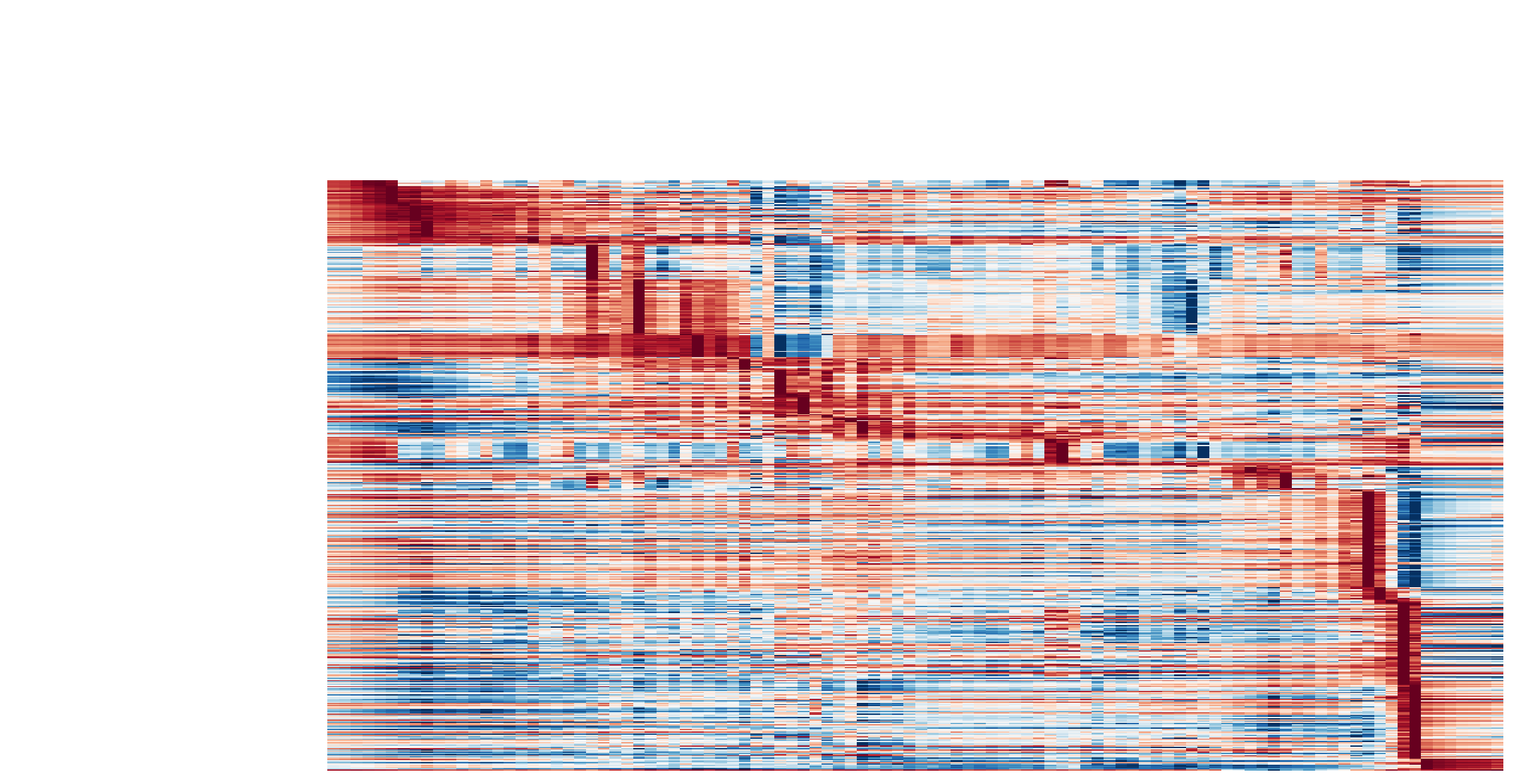
The kinetic heatmap shown below indicates that there are a few distinct stages of gene expression changes (or velocity, acceleration, curvature, etc.) during zebrafish pigmentation.
dyn.ext.ddhodge(adata, basis='pca')
|-----> graphizing vectorfield...
|-----------? nbrs_idx argument is ignored and recomputed because nbrs_idx is not None and return_nbrs=True
|-----------> calculating neighbor indices...
|-----> [ddhodge completed] completed [28.0423s]
transition_genes = adata.var_names[adata.var.use_for_transition]
Visualize the gene expression dynamics as a function of vector field based pseudotime (x-axis).
dyn.pl.kinetic_heatmap(adata,
genes=transition_genes,
tkey='pca_ddhodge_potential',
gene_order_method='maximum',
mode='pseudotime',
color_map='viridis',
yticklabels=False,
)
Note that if you want to visualize the gene expression for a specific cell lineage, you can subset the adata via something like (the same applies to other kinetic heatmaps):
Let us check the melanophore lineage by cross referencing the
vector-field based pseudotime and the streamline plots, overlaied with
cell-type annotations.
dyn.pl.streamline_plot(adata, color=['pca_ddhodge_potential', 'Cell_type'])
|-----------> plotting with basis key=X_umap
|-----------> skip filtering Cell_type by stack threshold when stacking color because it is not a numeric type
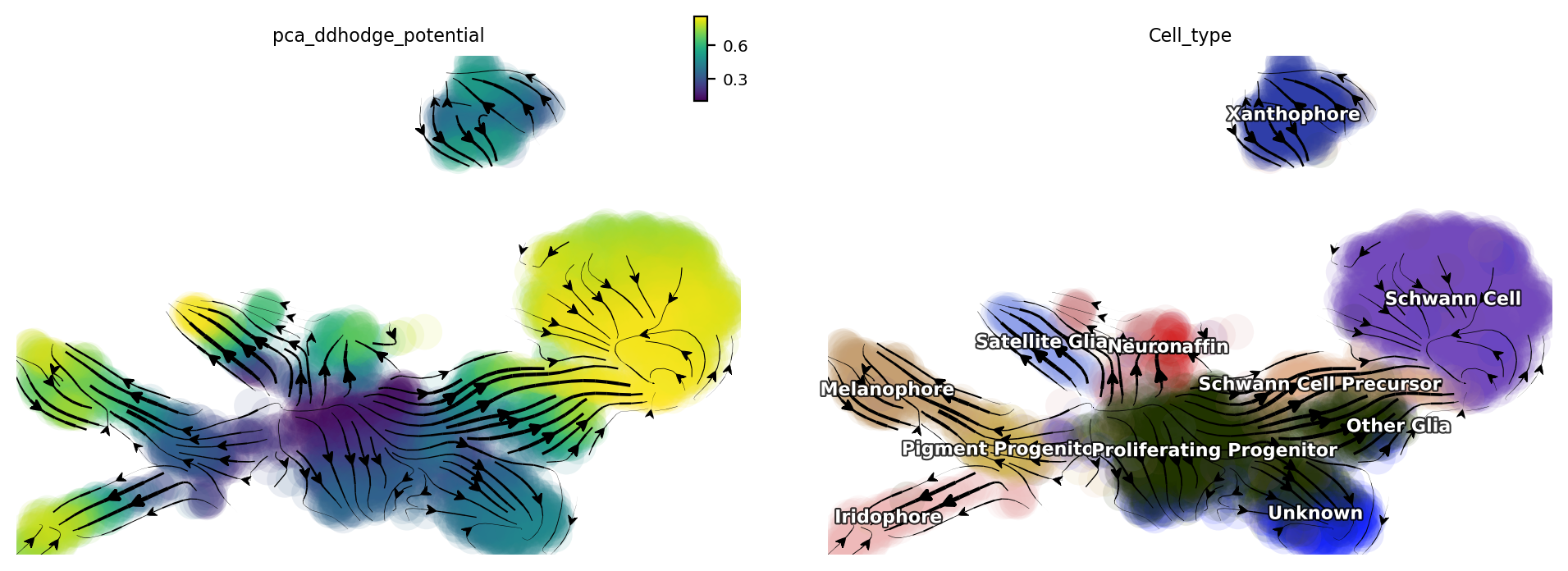
We can then collect cells from Proliferating Progenitor,
Pigment Progenitor, Melanophore that forms the melanophore
lineage by subseting adata object. This adata subset is then used to
visualize the expression kinetic heatmap for the melanophore lineage.
subset = adata[adata.obs.Cell_type.isin(['Proliferating Progenitor', 'Pigment Progenitor', 'Melanophore'])]
dyn.pl.kinetic_heatmap(subset,
genes=transition_genes,
tkey='pca_ddhodge_potential',
gene_order_method='maximum',
mode='pseudotime',
color_map='viridis',
yticklabels=False,
)
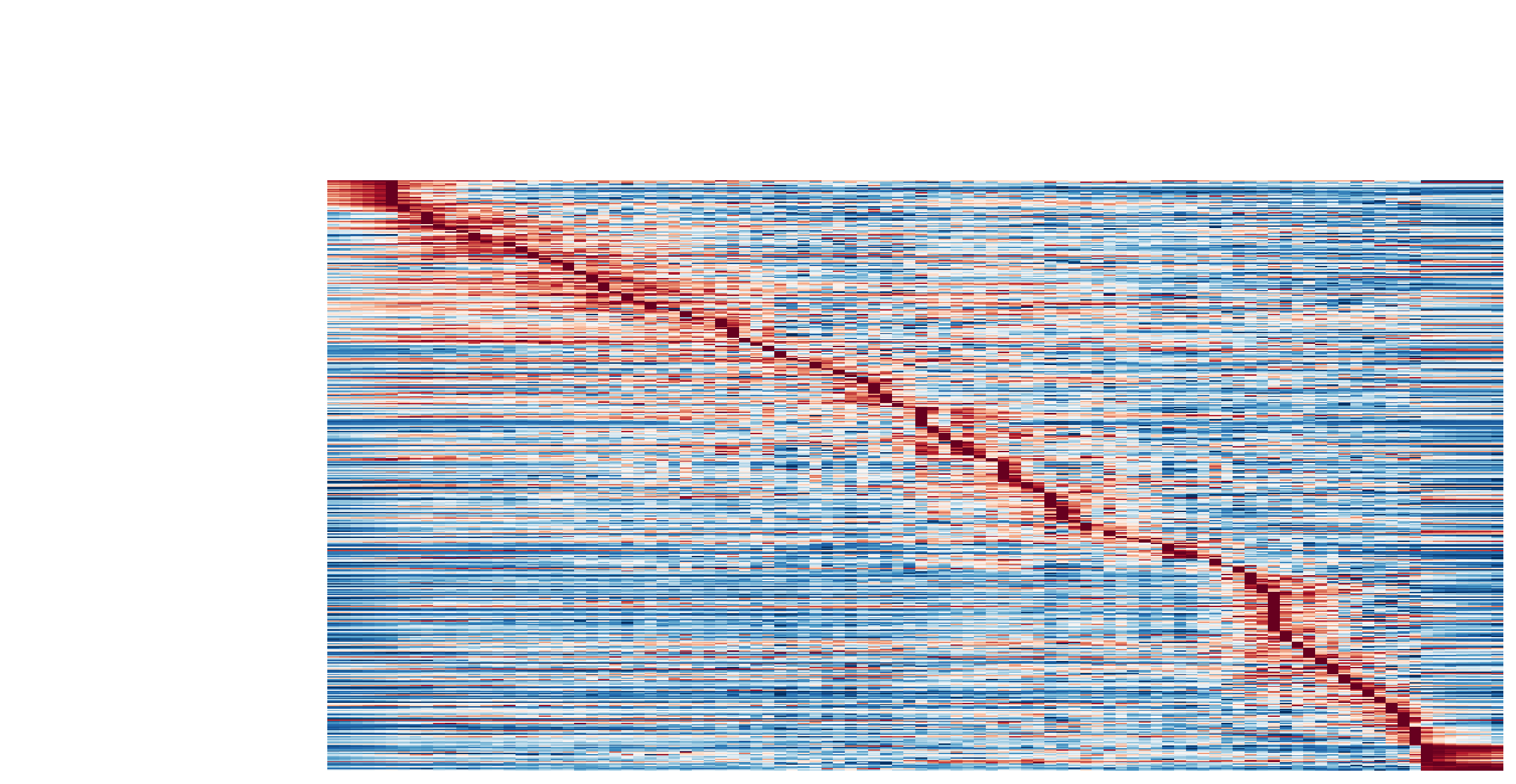
Visualize the gene velocity dynamics as a function of vector field based pseudotime (x-axis).
dyn.pl.kinetic_heatmap(adata,
genes=transition_genes,
tkey='pca_ddhodge_potential',
gene_order_method='maximum',
layer='velocity_S',
mode='pseudotime',
color_map='RdBu_r',
yticklabels=False,
)
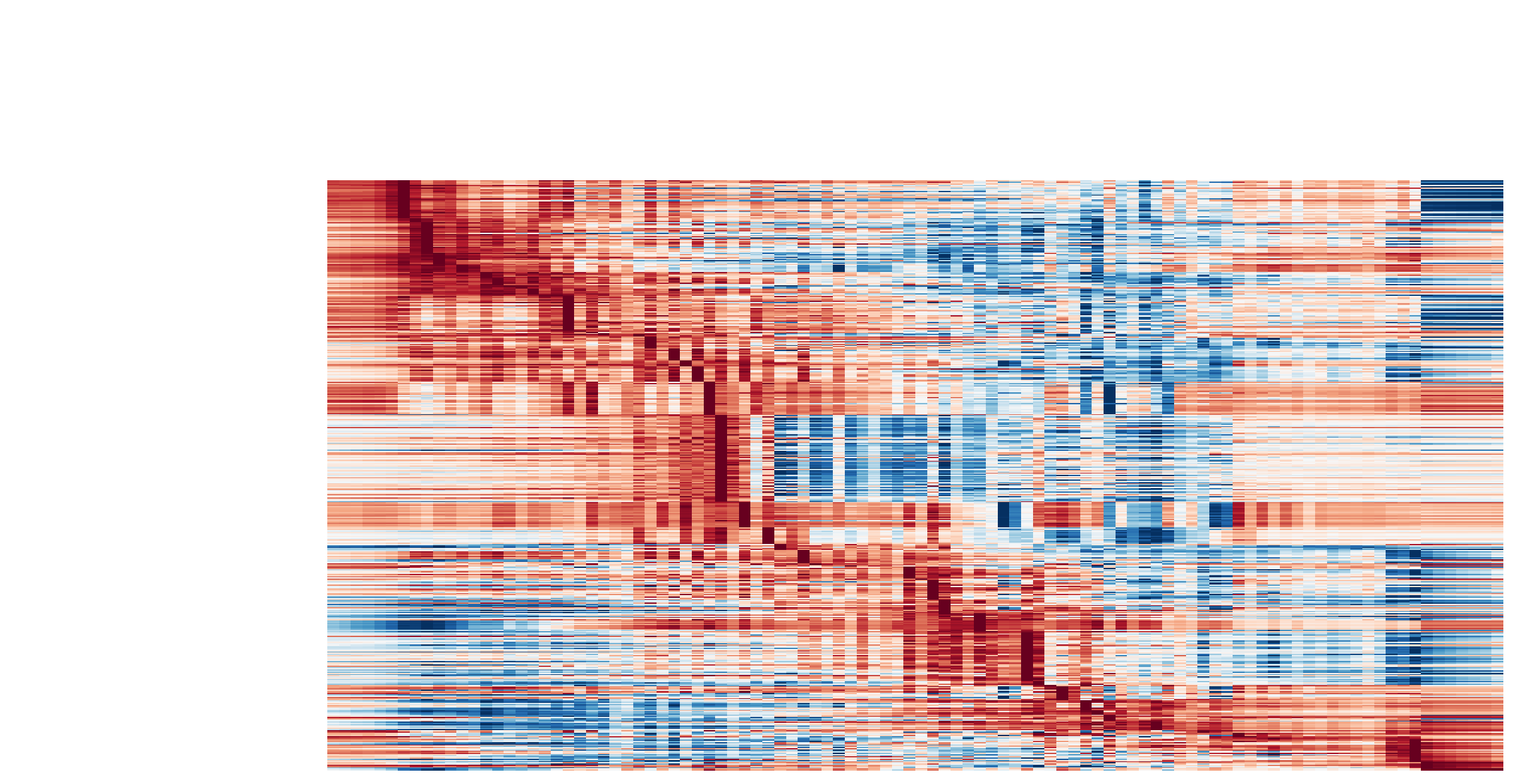
Visualize the gene acceleration dynamics as a function of vector field based pseudotime (x-axis).
dyn.pl.kinetic_heatmap(adata,
genes=transition_genes,
tkey='pca_ddhodge_potential',
gene_order_method='maximum',
layer='acceleration',
mode='pseudotime',
yticklabels=False,
color_map='RdBu_r')
Visualize the gene curvature dynamics as a function of vector field based pseudotime (x-axis).
dyn.pl.kinetic_heatmap(adata,
genes=transition_genes,
tkey='pca_ddhodge_potential',
gene_order_method='maximum',
layer='curvature',
mode='pseudotime',
yticklabels=False,
color_map='RdBu_r')
Build transition graph between cell states
When projecting high-dimensional RNA velocity vectors into low-dimensional space, dynamo builds a cell-wise transition matrix by translating the velocity vector direction and the spatial relationship of each cell to its neighbors to transition probabilities, similar to velocyto, etc. dynamo uses a few different kernels to build such a transition matrix which can then be used to run Markov chain simulations, as we will demonstrate in future.
On the other hand, it is of great interests to obtain a transition graph between cell types (states). dynamo implements such a functionality with a few methods which effectively creates a model that summarizes the possible cell type transitions based on the reconstructed Markov transition matrix between cell or the vector field function.
To achieve this, we only need to build a state graph with
dyn.pd.state_graph in a specific basis for a specific grouping. For
example, we can use the vector field integration based method vf to
build a transition graph between different cell types:
%%capture
dyn.pd.state_graph(adata, group='Cell_type', basis='pca', method='vf')
|-----> Estimating the transition probability between cell types...
|-----> Applying vector field
|-----> [KDTree parameter preparation computation] in progress: 0.0000%|-----> [KDTree computation] completed [0.0030s]
|-----> [iterate groups] in progress: 100.0000%|-----> [iterate groups] completed [44.0507s]
|-----> [State graph estimation] completed [0.0009s]
Next, a state graph can be visualized with dyn.pl.state_graph.
dyn.pl.state_graph(adata,
color=['Cell_type'],
group='Cell_type',
basis='umap',
show_legend='on data',
method='vf');
|-----------> plotting with basis key=X_umap
|-----------> skip filtering Cell_type by stack threshold when stacking color because it is not a numeric type
<Figure size 640x480 with 0 Axes>

Save results
save ranking information to an excel file
dynamo provides an utility function to automatically save the ranking related data frames to an excel file with each ranking information saved to a separate sheet in the xlsx file.
dyn.export_rank_xlsx(adata, path="rank_info.xlsx")
|-----> saving sheet: rank_velocity_S
|-----> saving sheet: rank_abs_velocity_S
|-----> saving sheet: rank_acceleration
|-----> saving sheet: rank_abs_acceleration
|-----> saving sheet: rank_curvature
|-----> saving sheet: rank_abs_curvature
|-----> saving sheet: rank_div_gene_jacobian_pca
Save data with pickle dumping or pandas dataframe to_csv
In addition, you can directly either export data to a csv file via:
adata.uns['rank_acceleration'].to_csv('./zebrafish_vf_rank_acceleration.csv')
Alternatively, you can save the data via pickle dump:
import pickle
pickle.dump(adata.uns['rank_acceleration'], open('./zebrafish_vf_rank_acceleration.p', 'wb'))
pickle.dump(full_reg_rank, open('./zebrafish_vf_full_reg_rank.p', 'wb'))
_acceleration_rank = pickle.load(open('./zebrafish_vf_rank_acceleration.p', 'rb'))
_acceleration_rank.head(2)
Dynamo save utility
Note that there may be intermediate results stored in adata.uns that can
may lead to errors when writing the h5ad object. For now, we suggest
users to call dyn.cleanup(adata) first to remove these data objects
before saving the adata object.
dyn.cleanup(adata);
call AnnData write_h5ad to save the entire adata information.
adata.write_h5ad("./tutorial_processed_zebrafish_data.h5ad")
You can load in the data later if need:
_adata = dyn.read_h5ad(("./tutorial_processed_zebrafish_data.h5ad"))

